

It does not essentially provide the value of the function at x. The limit of a function f(x) defines the behavior of the function near to a specific x value. It is used in describing some of the significant theories in calculus such as the definite integral of a function, a derivative of a function, and continuity. The idea of a limit of a function is vital to the study of calculus. The limits calculator solves the limits with steps and shows you each phase of the calculation. The domain of definition is the set of positive reals, 1 being excluded.Limit calculator is used to evaluate the limit functions with respect to a specified variable. When `x` becomes larger, `1/(x+1) `becomes smaller and closer to 0.Įxamples of limit calculation with an indeterminate formĬalculate `lim_(x -> 1) (x-1)/(sqrt(x) -1) ` When `x` gets closer to 0, `x^2` also approaches 0 (on the positive side because `x^2 >= 0`), so `1/x^2` becomes larges and tends to `+oo`.Įxample 3: case of a determinated form (`1/(+oo) `) When `x` is closer to 0, then `x^2` also approaches 0 so `x^2+1` is closer to 1.Įxample 2: case of a determinated form (`1/(0+) `) Here are some examples:Įxample 1: a simple case of direct substitution In this case we replace x with infinite (precisely by large positive numbers for `+oo` and large negative numbers for `-oo`) to see the behavior of the function. Apply the hospital rule that can be stated as follows: Factor the term of the highest degree in a polynomial (case of a ratio of two polynomials) Here are the most used techniques to lift indeterminacy: Q (a non-zero number with undeterminated sign),ĭeterminate forms: addition and subtraction N (as negative) a non-zero negative real number,

P (as positive) a non-zero positive real number, In the latter case, indeterminacy should be lifted by applying techniques such as simplification, conjugate multiplication, etc.
#Limits calculus calculator how to
How to calculate the limit of a function ?ĭirect substitution calculation (case `x -> a`)ĭirect substitution is the first technique to try, that is to replace x with 'a' to see how the function behaves at the neighborhood of 'a'.ĭirect substitution can lead to either a determinated form (or defined form) or an indeterminate form (or indefinite form). It is therefore important to check the limit at both sides. This distinction is necessary because for some functions, the 'right-hand limit' can be different from the 'left-hand limit' at a certain x-value. The limit obtained in this case is called left-hand limit. gets 'close' to 'a' while remaining less than a, we note this `x -> a-`. Similarly, x can tend to 'a' from the left i.e. The limit obtained in this case is called right-hand limit.
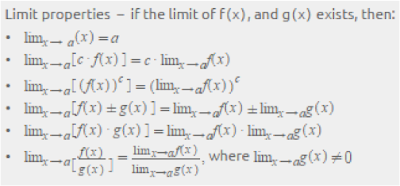
gets closer to 'a' while remaining greater than 'a', we note this `x -> a+`. In the above definition, we can distinguish two ways for x-values to tend to 'a' : `lim_(x -> a) f(x) = +oo`, means that when x gets closer to 'a' then, the value of the function becomes bigger (tends to positive infinity, this is the case of a vertical asymptote). `lim_(x -> +oo) f(x) = L`, means that when x becomes very large (tends to infinity), then the value of the function get very close to L (case of horizontal asymptote).

The above definition and notation remain valid if 'a' and/or "L" are replaced by positive infinity or negative infinity. This means that when x becomes very close to 'a' then, the value of f function becomes very close to L. If the limit of f(x) is equal to L when x tends to a, with a and L being real numbers, then we can write this as, The limit of a function at a given point tells us about the behavior of that function when x approaches that point without reaching it. You may use theses functions in the expression of f(x) In this case, enter x in the “main variable” fieldįor multiply operator, enter a*b not a.b nor ab. A function can have one or more variables, but only one main variable.Ī variable is a single lowercase or uppercase letter.Ī function f with one main variable : f(x) = 4*xĪ function g with one main variable x and a secondary parameter m,


 0 kommentar(er)
0 kommentar(er)
